こんにちは。ディレクターのJackです。ディレクター連載「統計入門のはじめ」の第4回は、相関係数についてです。
第3回では、「散布図と相関」についてご紹介しました。
復習:散布図とは?
まず、散布図についておさらいです。
散布図とは、2種類の項目を縦軸と横軸にとり、プロット(打点)により作成される図のことである。品質管理における「QC7つ道具」の1つとして数えられている。 引用:IT用語辞典バイナリ
相関(2つのデータの関係)を知るために利用する図のことです。これを相関図と呼びます。
相関図でもデータの関係性を把握することはできるのですが、しっかりと根拠を提示するためにも定量的に、データの関係性を把握できたらなお良いですよね。
それを実現するのが、「相関係数」です。
相関係数とは
さっそく、本題です。
相関係数とは、なんでしょうか?
検索してみました。
〘数〙 二つの変量間の相関関係の程度を表す数値。
引用:流通用語 Weblio辞書
変量間? なに、それ?
簡単にいうと「2つの値の関係の強さを示す数値」のことを指します。例えば、相関係数を使えば「アンパンを買っている人は、牛乳も一緒に買うことが多い」といったような傾向を、見つけることができるかもしれません。
相関係数の言葉を理解した上で「相関係数の求め方」を、一緒に勉強していきましょう。
今回は、R言語という統計解析用のプログラミング言語を利用し、相関係数を求めていきたいと思います。
R言語とは?
まず、R言語とは何かを確認してみましょう。本連載では、R言語を利用する記事もありますので、都度紹介させていただきますね!
R言語(あーるげんご)はオープンソース・フリーソフトウェアの統計解析向けのプログラミング言語及びその開発実行環境である。
R言語 – Wikipedia
オープンソースで提供されている統計解析向けのプログラミング言語です。
R: The R Project for Statistical Computing というサイトにて、ダウンロードできますのでインストールを済ませておきましょう。
ではさっそく、R言語を利用し相関係数を求めてみましょう。
R言語で相関係数を求めてみる
さっそく、R言語を利用して、相関係数を求めてみましょう。
今回利用するデータは、気象情報のデータです。こちらは、データを把握する統計入門〜散布図(相関図)について〜で利用したデータですね。
2016年6月1日〜2016年6月15日の東京の最高気温と平均湿度で相関係数を算出してみます。
また、本データは、気象庁のHPからデータはダウンロード可能です。
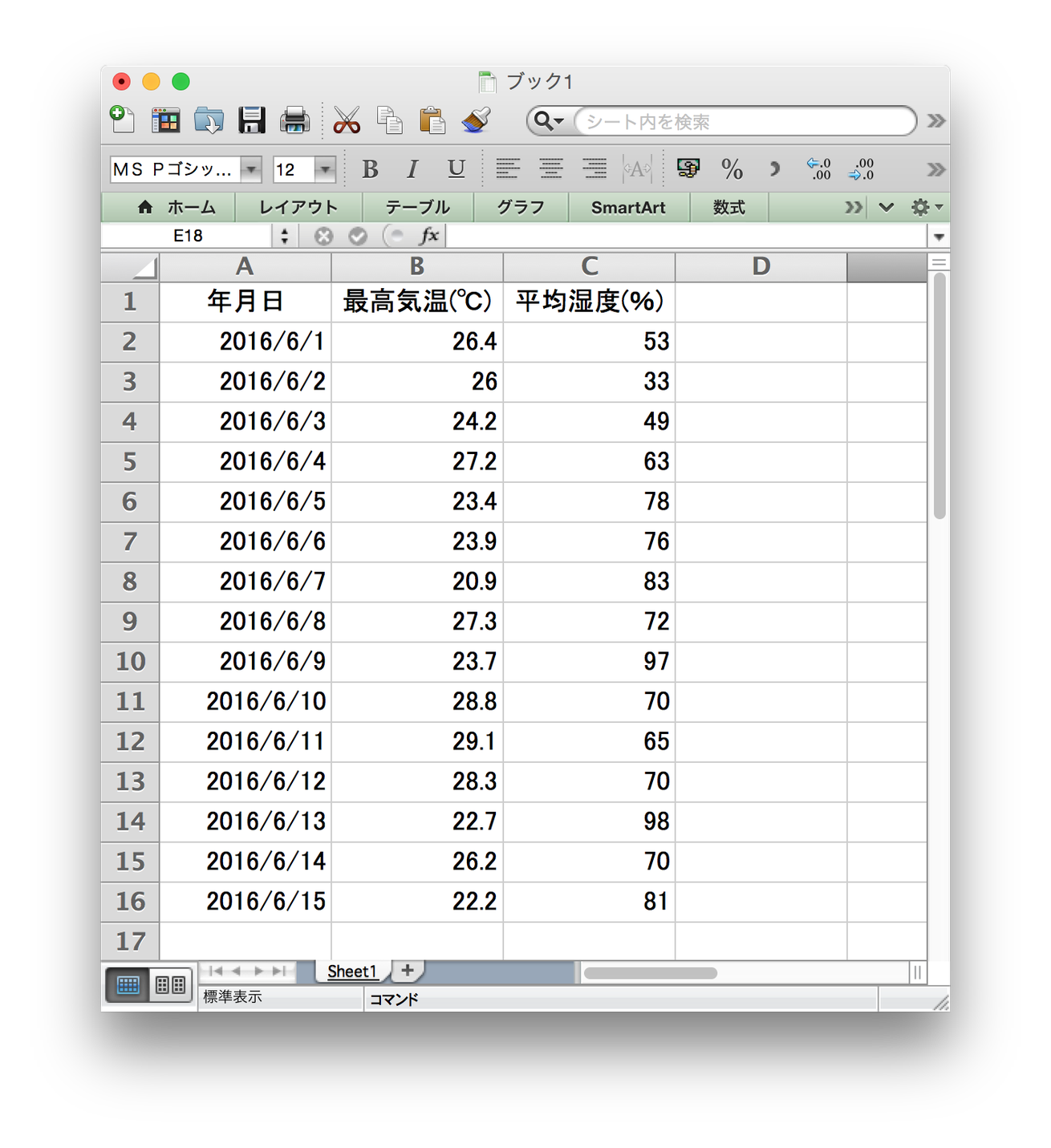
Excelシートの内容を、R言語のベクトル形式にすると下記のようになります。
xが最高気温、yが平均湿度となります。
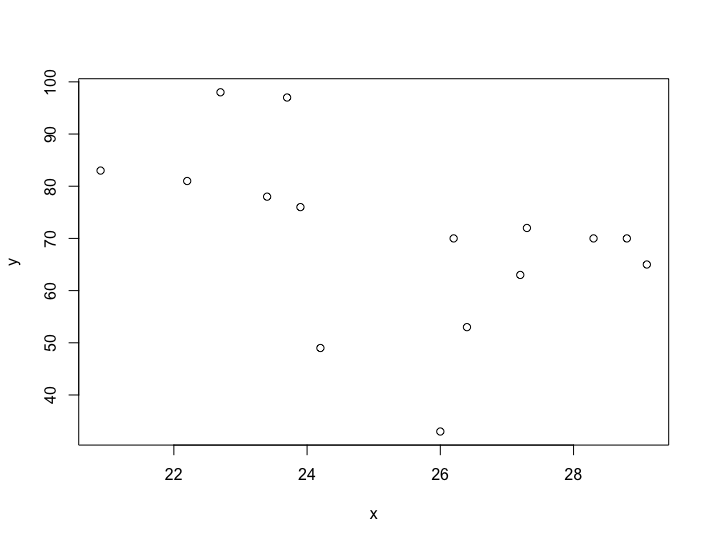
> x <- c(26.4,26,24.2,27.2,23.4,23.9,20.9,27.3,23.7,28.8,29.1,28.3,22.7,26.2,22.2) > y <- c(53,33,49,63,78,76,83,72,97,70,65,70,98,70,81)散布図を求めると、下記のようになります。plot(x, y)というコマンドで簡単に出力する事ができます。
んー、これだけ見ると無相関な感じがします。相関係数を求めて、しっかりと数値として根拠を出してみましょう。
相関係数を求めてみる
相関係数を求めるには、Rコンソールにてcorというコマンドを実行してください。
これで簡単に2つのデータの相関係数を求める事ができます。> cor(x, y, method="pearson") [1] -0.4620266相関係数は、-0.4620266という値になりました。
相関係数の大きさ(絶対値)と相関の程度の表現の対応関係は、下記が目安となります。
| 1.0≧|R|≧0.7 | 高い相関がある |
|---|---|
| 0.7≧|R|≧0.5 | かなり高い相関がある |
| 0.5≧|R|≧0.4 | 中程度の相関がある |
| 0.4≧|R|≧0.3 | ある程度の相関がある |
| 0.3≧|R|≧0.2 | 弱い相関がある |
| 0.2≧|R|≧0.0 | ほとんど相関がない |
おお! 無相関だと思っていましたけど、そこそこ相関がありそうですね。
次回は求めた相関係数に、意味があるのかどうかを決定する「無相関検定」に挑戦していきたいと思います!
おわりに
いかがでしたか?
今回は、相関係数について勉強しました。これで、2つの相互関係の程度を数値として表す事ができるようになりました。
これで、少し踏み込んで、データの解析ができるようになりましたね!
LIGはWebサイト制作を支援しています。ご興味のある方は事業ぺージをぜひご覧ください。