データを把握する統計入門〜散布図（相関図）について〜

こんにちは。ディレクターのJack (@y_kazuhiko) です。ディレクター連載「統計入門のはじめ」の第３回は、散布図と相関についてです。

統計？　散布図？　相関？　いやーなんか急にハードル上がっている感がありますよね。安心してください。僕もひとつずつ勉強しながら記事を書いていますので、一緒に勉強していきましょう。

では、さっそく本題です。

改めて、統計とは？

第1回の記事で、LIGの統計王ことともぞう氏が説明をしてくれています。

統計王曰く、

集めたデータ(数字)を整理することです。
整理するというのは、データから特徴を見出すことです。

例えば小さいところでいうと平均も統計の手法のひとつです。
平均を出すことで特徴をつかめますね。

との事です。

ふむふむ、ざっくり言うと、たくさんのデータから何かしらの特徴を見出すということですね。

では、特徴を見出す手法は何があるのでしょうか？　そこで用いられるのが、散布図です。（もちろん他にも色々ありますよ！）

散布図とは

散布図とはなんでしょうか？　ちょっと調べてみました。

散布図とは、2種類の項目を縦軸と横軸にとり、プロット（打点）により作成される図のことである。品質管理における「QC7つ道具」の1つとして数えられている。　引用：IT用語辞典バイナリ

んんん？　なんとなーく分かりますけど、いまいちよく分かりません…。
簡単にいうと、相関（2つのデータの関係）を知るために利用する図のことです。これは相関図とも呼びます。

また散布図（相関図）には3パターンありますので、覚えておきましょう。

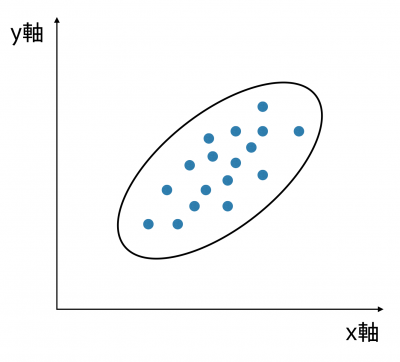
正の相関

一方の数値が大きくなると、他方の数値も大きくなる。

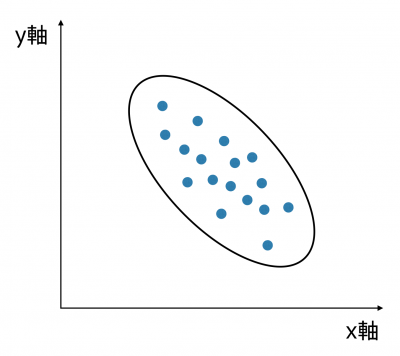
負の相関

一方の数値が大きくなると、他方の数値が小さくなる。

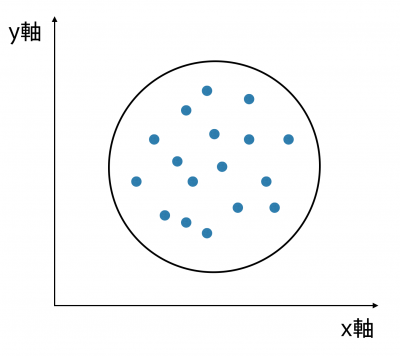
無相関

2つの数値に明白な関係が見られない。

実際にやってみる

実際の例をもとに一緒に勉強してみましょう。

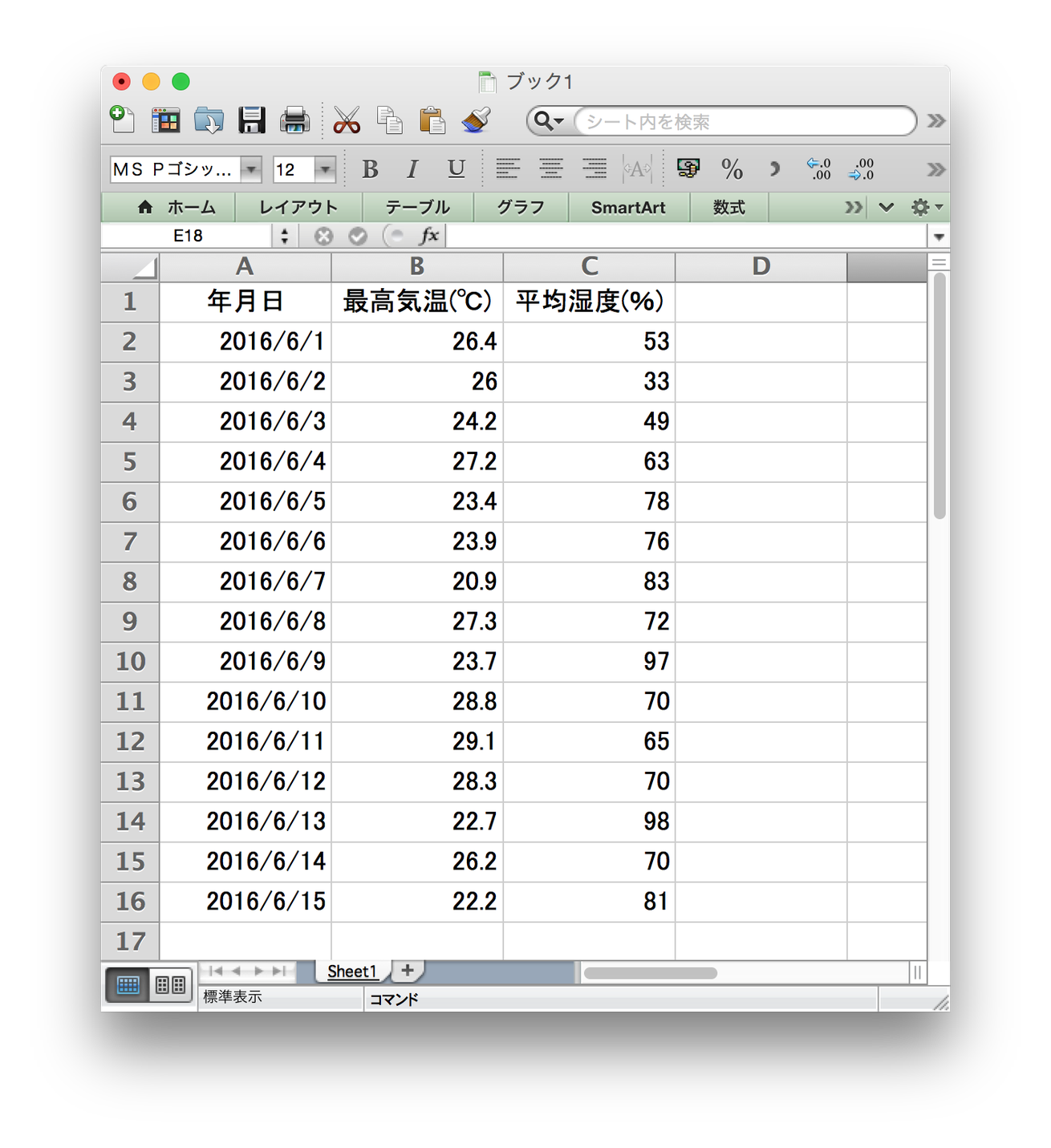
2016年6月1日〜2016年6月15日の東京の最高気温と平均湿度の関係を例にしてみます。利用するデータは下記の通りです。
気象庁のHPからデータはダウンロード可能です。

最高気温と平均湿度の関係の散布図は下記のとおりです。

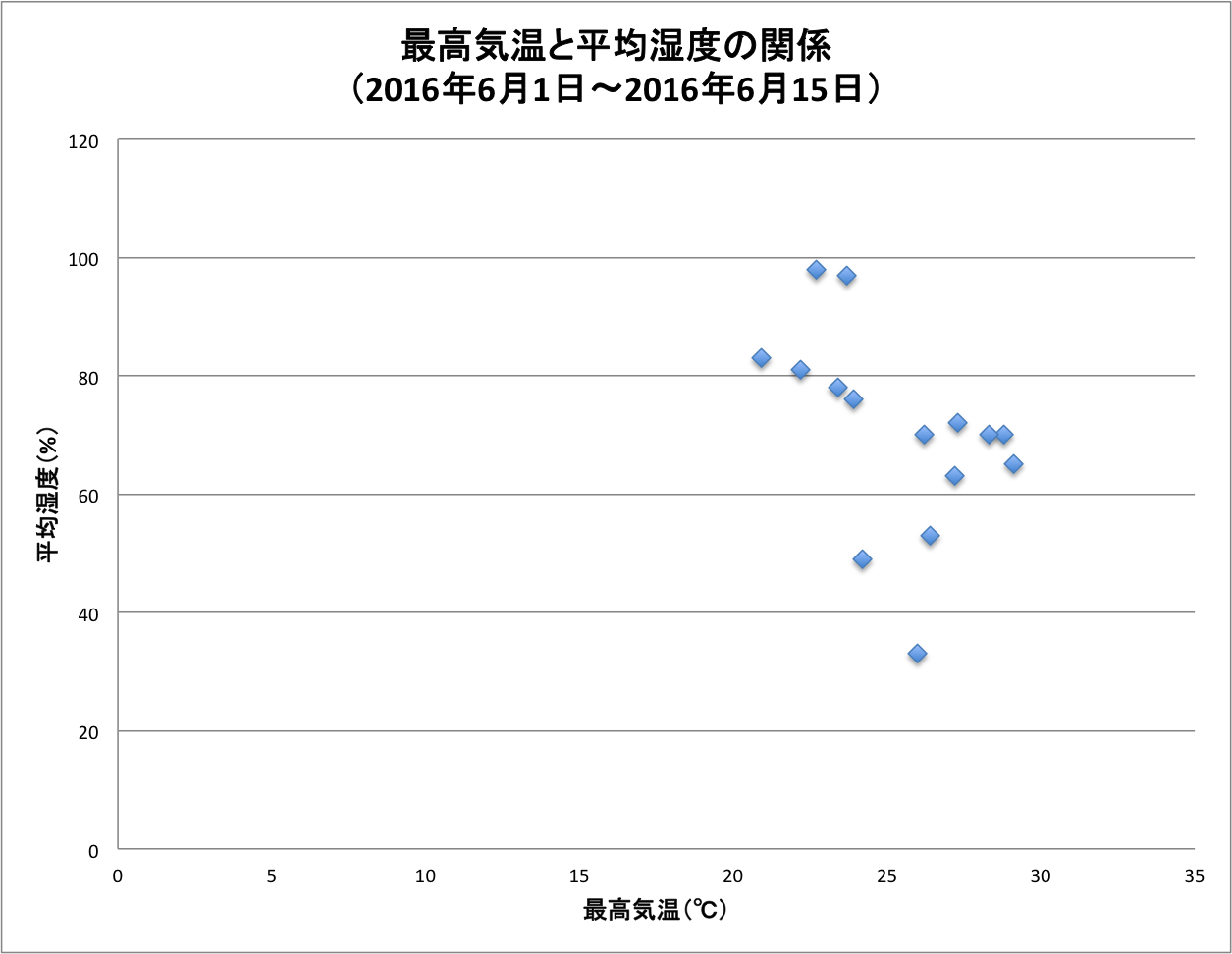
この散布図から見てわかるように、最高気温と平均湿度は「無相関」であることがわかります。
仮に、このデータが最高気温が高い場合に、平均湿度も高くなると「正の相関」となります。その逆で、最高気温が高く、平均湿度が低い場合は「負の相関」となるのです。

おわりに

今回は、散布図（相関図）について、勉強しました。これで、データの関係を把握することができるようになりましたね。
ただし、散布図や平均を見ただけでは、2つの値のおおまかな関係しか分からず、「強く関わりなのか」もしくは「弱い関わりなのか」分かりません。
そこで、2つの相互関係の程度を数値として表したのが、「相関係数」です。
次回は、相関係数についてあお話できればと思います。

LIGはWebサイト制作を支援しています。ご興味のある方は事業ぺージをぜひご覧ください。