こんにちは。ディレクターのJackです。ディレクター連載「統計入門のはじめ」の第7回は、無相関検定についてです。
徐々に難易度が上がってきましたね。
今回はR言語という統計用のプログラミング言語を使って、学んでいきたいと思います。
R言語とは?
まず、R言語を確認してみましょう。みんな大好きWikipediaで調べてみます。
R言語(あーるげんご)はオープンソース・フリーソフトウェアの統計解析向けのプログラミング言語及びその開発実行環境である。
R言語 – Wikipedia
オープンソースで提供されている統計解析向けのプログラミング言語です。
R: The R Project for Statistical Computing というサイトにて、ダウンロードできますのでインストールを済ませておきましょう。
また、R言語の基礎を学ぶには、下記サイトがおすすめですので、一通り目を通しておくと良いかもしれません。
さて、本題の「無相関検定」のお話に移ります。
そもそも、無相関検定って?
無相関検定とは「ある標本の相関係数を求めた際に、その相関係数に意味があるのかどうかを決定すること」を指します。
標本から得られた相関係数が大きいからといって、安心してはいけません。
そもそも、それが母集団で成立するかは分からないからです。不確実性が非常に高いですね。
無相関検定をおこなう際に、覚えておくべき用語があります。それは「帰無仮説」という用語です。
帰無仮説とは、母集団の相関係数が0(ゼロ)であると過程することです。
もし、この帰無仮説が否定されれば、その反対である「母集団の相関係数が0(ゼロ)ではない」ということが受け入れられることになります。
この仮説を否定することを「棄却」、受け入れることを「採択」と呼ぶのです。
今回は計算式は割愛し、無相関検定で求めた相関係数が意味があるのかどうかを、一緒に見ていければと思います。
(数式ばかりだと、疲れちゃいますもんね…)
R言語で無相関検定をやってみる
さっそく、R言語を使って無相関検定をやってみましょう。
今回利用するデータは、気象情報のデータです。
2016年6月1日〜2016年6月15日の東京の最高気温と平均湿度で相関係数を算出し無相関検定をおこないます。
データは気象庁のHPからダウンロード可能です。
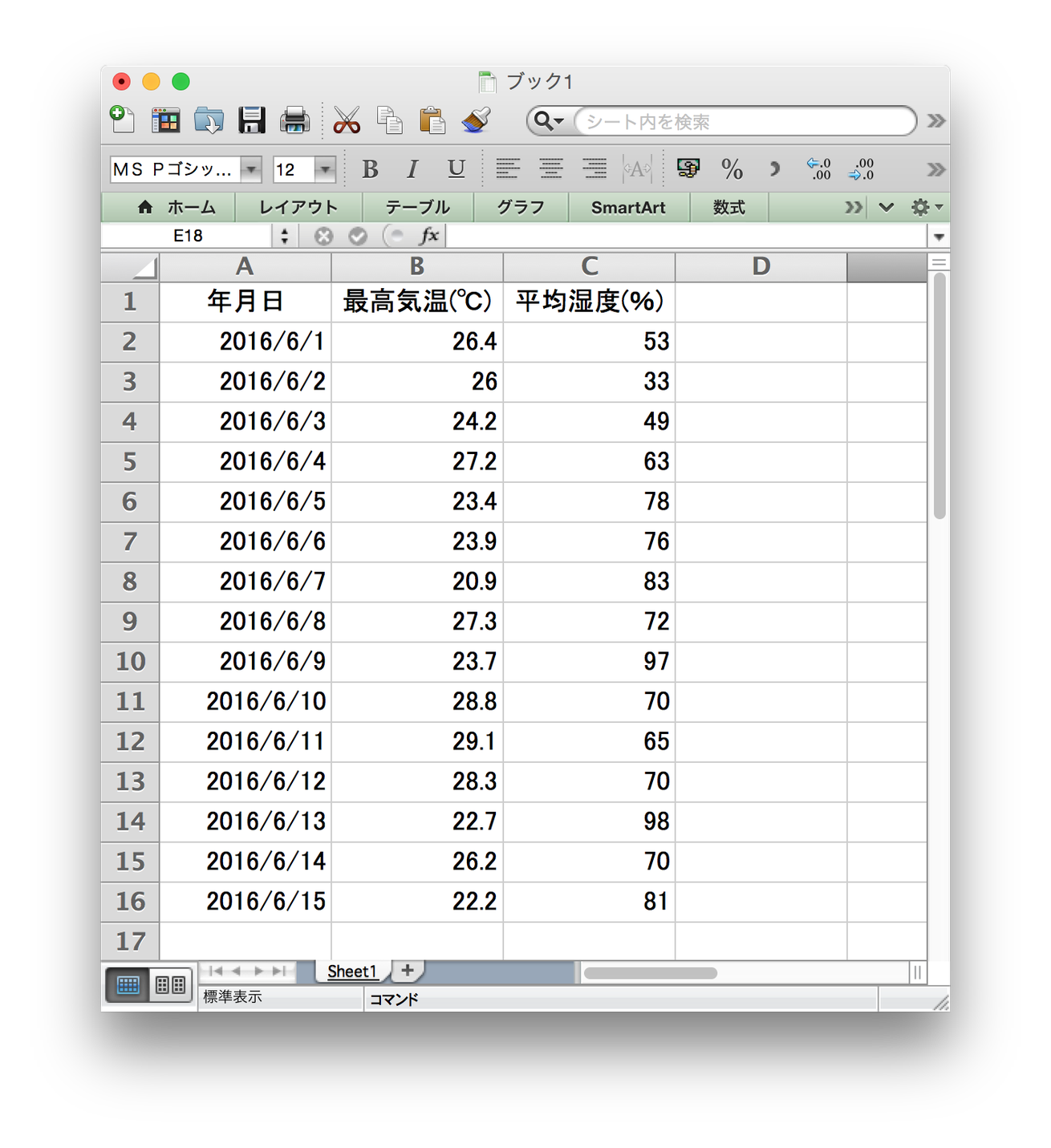
Excelシートの内容を、R言語のベクトル形式にすると下記のようになります。
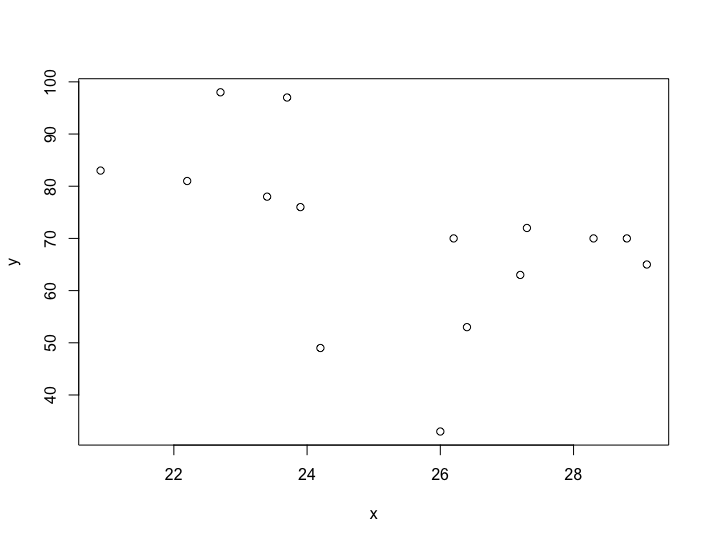
xが最高気温、yが平均湿度となります。
> x <- c(26.4,26,24.2,27.2,23.4,23.9,20.9,27.3,23.7,28.8,29.1,28.3,22.7,26.2,22.2) > y <- c(53,33,49,63,78,76,83,72,97,70,65,70,98,70,81)散布図を求めると、下記のようになりあます。plot(x, y)というコマンドで簡単に出力することができます。
相関係数を求めてみる
相関係数を求めるには、Rコンソールにてcorというコマンドを実行してください。
引数のmethodにpearsonを指定することで、ピアソンの積率相関係数を求めることができます。> cor(x, y, method="pearson") [1] -0.4620266相関係数は、-0.4620266という値になりました。
では、-0.4620266という相関係数に意味があるのかどうかを確認していきたいと思います。無相関検定を実施する
無相関検定をおこなうには、Rコンソールにてcor.testというコマンドを実行します。
> cor.test(x, y, method="pearson") Pearson's product-moment correlation data: x and y t = -1.8784, df = 13, p-value = 0.08294 alternative hypothesis: true correlation is not equal to 0 95 percent confidence interval: -0.78782723 0.06581275 sample estimates: cor -0.4620266いろいろと値が出力されてきましたね。これだけでは、よく分からない! なので、1つずつ一緒に見ていきましょう!
今回の無相関検定の結果、
- 相関係数はr=-0.4620266
- 母集団相関係数pに関する検定を行った結果、t値 = -1.8784、df(自由度) = 13, p-value(p値) = 0.08294
というような結果が得られました。
注目すべきは、p値(p-value)です。
p値とは、結果が統計的に有意かどうかを判断する際に利用される値です。
仮説検定ではよく使われている値ですね!
今回の結果は、p値が有意水準0.05(5%)より大きいので2つの変数「最高気温」と「平均湿度」の間には有意な相関があるとはいえないという結論となります。
-0.4620266という相関係数が起こる確率は、5%よりも大きいことが分かり、母集団の相関係数が0(ゼロ)であることを否定できないため、帰無仮説を採択することとなります。
つまり、今回求めた相関係数は、意味のある相関係数であるとはいえないという結論に至ります。
おわりに
今回は、R言語を利用しながら無相関検定について勉強しました。これで、求めた相関係数に意味があるのかどうかを把握することができますね。
次回は、別のデータを使って分析してみたいと思いますので、お楽しみに!
LIGはWebサイト制作を支援しています。ご興味のある方は事業ぺージをぜひご覧ください。